Chord Formulas: Fast-track Your Comping

Chord formulas can help you not only to play chords in any key, but they can also help you to understand chords on a different level.

We can create formulas in a few ways: the diatonic formulas and the chromatic formulas.

The big difference between those is:

• With diatonic formulas, you will know the mode and the key in which the chord is presented. But it will require you to be intimately familiar with the scale in order to play the chord by the formula.
• With chromatic formulas, you will be able to play the correct notes of the chord even if all you have is the name of the chord. But it will not give you any information about the key or the mode it represents so you will need to look at the context of the surrounding chords to get that information.

For short term gratification, I think the chromatic formulas will be the most useful. And when combined with good knowledge of chord progressions and some practice on chord analysis, they will take you every step of the way.

This post will, therefore, focus on chromatic formulas.

For a diatonic theory and diatonic chords of the major scale, please refer to my post:
► Basic Piano Chords – Theory – Diatonic Sequence

Looking for more information on inversions and smooth transitioning between chords? Then please check out my blog post ► Chord Inversions to Transition Chords Smoothly.

Chord Formula Chart

Because I know most people are here just for the chart, I will start off with that. However, for those who don’t know how to read all of this mumbo-jumbo I do explain it further down.

Major Formulas

Chord Type	Symbol	Formula
Major	M, Maj	1-3-5
Added Fourth	add4	1-3-4-5
Sixth	6	1-3-5-6
Six Nine	6/9	1-3-5-6-9
Major 7th	Maj7	1-3-5-7
Major Ninth	Maj9	1-3-5-7-9
Major Eleventh	Maj11	1-3-5-7-(9)-11
Major Thirteenth	Maj13	1-3-5-7-(9)-(11)-13
Major seven sharp eleventh	Maj7#11	1-3-5-7- #11
Major Flat Five	–	1-3-b5

Minor Formulas

Chord Type	Symbol	Formula
Minor	m	1-b3-5
Minor added fourth	madd4	1-b3-4-5
Minor sixth	m6	1-b3-5-6
Minor seventh	m7	1-b3-5-b7
Minor added ninth	madd9	1-b3-5-9
Minor six add nine	m6/9	1-b3-5-6-9
Minor ninth	m9	1-b3-5-b7-9
Minor eleventh	m11	1-b3-5-b7-(9)-11
Minor thirteenth	m13	1-b3-5-b7-(9)-(11)-13
Minor/Major seventh	m/Maj7	1-b3-5-7
Minor/Major ninth	m/Maj9	1-b3-5-7-9
Minor/Major eleventh	m/Maj11	1-b3-5-7-(9)-11
Minor/Major thirteenth	m/Maj13	1-b3-5-7-(9)-(11)-13
Minor seven flat fifth or half-diminished	m7-5 or ø	1-b3-b5-b7

Dominant Formulas

Chord Type	Symbol	Formula
Seventh	7	1-3-5-b7
Ninth	9	1-3-5-b7-9
Eleventh	11	1-(3)-5-b7-(9)-11
Thirteenth	13	1-3-5-b7-(9)-(11)-13
Seven sharp five	7#5	1-3-#5-b7
Seven flat five	7b5	1-3-b5-b7
Seven flat ninth	7b9	1-3-5-b7-b9
Seven sharp ninth	7#9	1-3-5-b7-#9
Nine sharp five	9#5	1-3-#5-b7-9
Nine flat five	9b5	1-3-b5-b7-9
Seven sharp five sharp nine	7#5#9	1-3-#5-b7-#9
Seven sharp five flat nine	7#5b9	1-3-#5-b7-b9
Seven flat five sharp nine	7b5#9	1-3-b5-b7-#9
Seven flat five flat nine	7b5b9	1-3-b5-b7-b9
Seven sharp eleven	7#11	1-3-5-b7-#11

Symmetrical Formulas

Chord Type	Symbol	Formula
Diminished	dim (° )	1-b3-b5
Diminished Seventh	dim7 (°7)	1-b3-b5-bb7
Augmented	aug (+)	1-3-#5

Miscellaneous Formulas

Chord Type	Symbol	Formula
Fifth	5	1-5
Flat Fifth	-5	1-b5
Suspended Fourth	sus4	1-4-5
Suspended Second	sus2	1-2-(9)-5
Sharp Eleven	#11	1-5-#11

How to Use These Chord Formulas

There are two ways you could look at these formulas:

• Using interval theory which for me is the preferred method. The formulas show the intervals that are played on top of the root note, where 1 is the root note, and all other numbers are the intervals above that root.(Don’t worry, I will clarify exactly what that means)
• Using the major scale that is built from the root note indicated by the 1. All numbers in the formula then become the scale degree of that major scale. All numbers without adjustments (flat or sharp) are then diatonic notes of that major scale, whereas all flattened or sharpened numbers are chromatic adjustments of the diatonic notes of the major scale. (Sounds complex, but I will also clarify)

I say the first one has my preference, but to be honest, both have their merits.

The first method allows for very fast deciphering of the chord that will allow you to play the clustered chord instantly.

The second method will give you the absolute note names, which means you can easily invert the chords on the fly and play the chords either clustered or spread.

Formulas Using Intervals

Using intervals is actually really easy. Which goes to show how vital interval theory is when it comes to learning music and learning an instrument.

If you want to know more about intervals in general, check out my blog post here:
► Music Theory: Intervals – How To Train Your Ears

When we use the symbols that we learned in the blog post about intervals mentioned above, things should actually become crystal clear.

Example: Minor 7 => 1 – b3 – 5 – b7

For example when we take the formula for a minor 7 chord: 1 – b3 – 5 – b7

Cm7

We can apply this to any root and I will start with the easiest one of all: Cm7

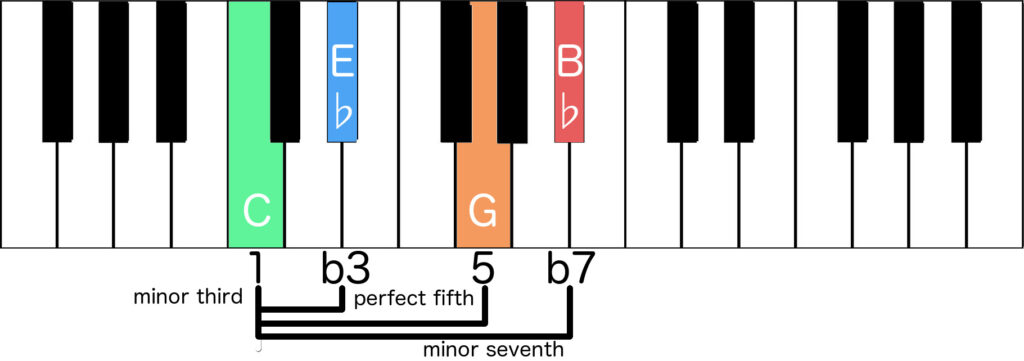
With the root (1) as C, the minor third (b3) as Eb, the perfect fifth (5) as G and the minor seventh (b7) as Bb
We now have all the notes of the Cm7 chord.

Dbm7

Another example of the same formula: Dbm7

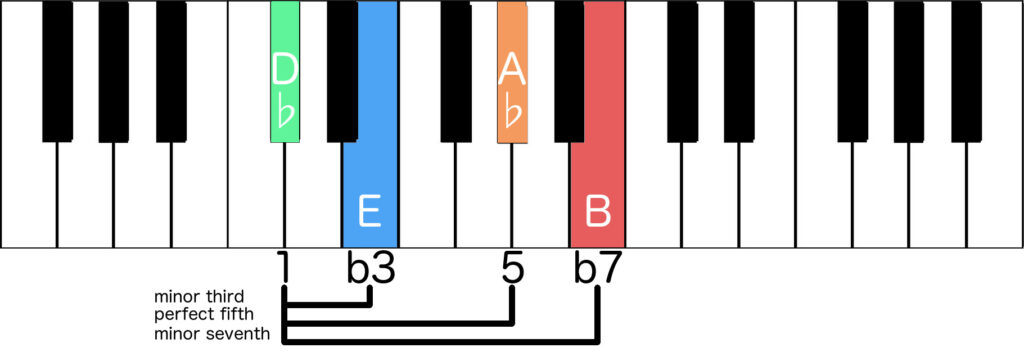
With the root (1) as Db, the minor third (b3) as E, the perfect fifth (5) as Ab and the minor seventh (b7) as B
We now have all the notes of the Dbm7 chord.

Using Intervals Really Is That Easy

Honestly, that is all you need to know if you work with intervals. It is that easy!

It does, however, mean that you need to know your intervals inside out. Using intervals, everything becomes easier 😀 and that is the big lesson to take away from this.

Formulas Using The Major Scale and Chromatic Adjustments

This is mostly a different point of view on working out the chord formulas. It involves a paradigm shift where we look at the numeric scale degrees of a major scale and adjust those notes by applying flats or sharps.

The great shift is that you will not be thinking about the intervals, but rather about the absolute notes in a given major scale. This does have the benefit that you can place those notes anywhere on your keyboard and you will be able to use spread voicings and inversions on the fly.

At the same time, it takes a lot of practice to be able to name the notes in real-time by numeric degree.

As an example, can you tell me quickly what is the 5th note of the Ab major scale? If you can, good on you! But you can see that this is something that will require a lot of time and effort to master.

Example: Minor 7 => 1 – b3 – 5 – b7

So let’s work out this example for Ab.

Abm7

We start by working out the Ab major scale. We (should) know the Ab major scale has a key signature of 4 flats: Bb, Eb, Ab and Db.

That gives us the major scale of Ab:

Note	Ab	Bb	C	Db	Eb	F	G
Degree	1	2	3	4	5	6	7

Then we apply our formula on this:

Note	Ab	Bb	C	Db	Eb	F	G
Degree	1	2	3	4	5	6	7
Formula	1		b3		5		b7
Result	Ab		Cb		Eb		Gb

With the root (1) as Ab, the flat third degree (b3) as Cb, the fifth degree (5) as Eb and the flat seventh degree (b7) as Gb
We now have all the notes of the Abm7 chord.

Why don’t we call Cb just B? Because they are the same note in principle…

We need to use every letter in the sequence. From Ab to B is a minor third interval. The alphabetical distance from A to B is only 2 and a third interval needs an alphabetical distance of 3. Cb is, therefore, the correct name of the note.

Em7

Let’s work this out using another root; the E.

Again we start by working out the E major scale. We (should) know that E major scale has a key signature of 4 flats: F#, C#, G# and D#.

That gives us the major scale of E, and we will work out the formula and the result in one go:

Note	E	F#	G#	A	B	C#	D#
Degree	1	2	3	4	5	6	7
Formula	1		b3		5		b7
Result	E		G		B		D

With the root (1) as E, the flat third degree (b3) as G, the fifth degree (5) as B and the flat seventh degree (b7) as D
We now have all the notes of the Em7 chord.

So Much Harder Than Intervals

I am sure you see the computations involved are far more complex than when we use the interval method. But this method reveals different information about our chord. Instead of counting semitones to get to an interval, we directly know the absolute note name and can play it anywhere on the keyboard.

One could argue that the interval method also gets you to the point where you know the absolute notes but it would involve one extra step of first playing or visualizing the note in its position within the clustered voicing of the chord. After that, you can also place those notes anywhere on the keyboard.

Why Bother?

Well even though it may not be clear right at this moment, there are a lot of reasons why in the end this method may turn out to be a lot faster and not as hard to remember as you think.

When you practice your scales, you will also be practising fingerings that are a direct reference to the degrees of the scale. Your muscle memory will get trained and it will start doing things that even your mind can’t follow.

If you want to know how that is possible, I have written a blog on how the brain works when you practice your instrument ► franspianostudio.me

What’s Next

Chords will really blow your mind once you start incorporating degrees and modes into your arsenal! If you think you know everything there is to know at this point… Think again! 😀

My next 3 blog posts will be about:

• Diatonic modes of the major scale. That is going to be a lot of fun because those will take your improvising and soloing to the next level.
• Chord substitution which in combination with the diatonic modes will make your improvisations sound like they come from another world! To infinity and beyond!!!
• The circle of fifths, because we need to get back to basics for the beginners. I can’t leave them out in the cold for too long.

Keep your eye on the walk people! More is coming soon!!!